1.问题描述
给定一个固定容量capacity的包,有数目(number)不定的物品,其中物品包括价值和重量,在给定容量的前提下,使得装入物品的价值最大。求出所装入物品的最大价值以及所装入物品的序号。
2.解决办法
利用动态规划法和回溯法来求此问题,其中回溯法是来求包的序号。动态规划法的核心思想是通过把大的问题分为很多的小问题,通过用大问题和小问题的递推关系把小问题解决了,最终得到大问题的解。当然,动态规划法是由记忆性的,它会把每次计算的结果保存下来,等到用到的时候直接调用,这样避免了很多重复计算。这也是动态规划法与分治法的区别。
由上可知,我们可以把背包问题的每一次的解,用一个二维表格来保存,然后最后的那个结果即为所求的解。
首先,建立一个二维数组wv[number][2],来存放物品的重量和价值。之所以这样做数组是为了方便单独取重量或价值,为后面所用
例如:
w v
2 3
3 4
(取重量时直接wv[0][i],只变i就可以了,价值类似。这样方便后面调用)
接下来我们来初始化上面所提到的表格sheet,这里我们来定义两个特殊的行和列。分别是sheet[i][0]=0,和sheet[0][j]=0
这两个行列分别代表当包的容量为0时,自然而然物品放不进去,所以为价值0,后一个表示由容量,但没放物品,所以价值也为0。这对后面初始化表格很重要,接下来求价值都是以这个行列为基础的。
接下来正式初始化表格,我们以这样的一个思路来解决问题:
(1)当物品的重量大于剩余容量时,此时包中原价值不变。
(2)当物品的重量小于剩余容量时,此时代表可以放入,但此时装入也不一定代表是最优值,所以就要比较原有的价值和放入后的价值,选取最优。
将上面两句话写成伪码可得两个条件,我们就以这两个条件填表sheet
if(wv[i-1][0]>j) {
sheet[i][j]=sheet[i-1][j];//此时价值不变,剩余容量也不变,和原有一样
}else {
sheet[i][j]=max(sheet[i-1][j],sheet[i-1][j-wv[i-1][0]]+wv[i-1][1]);//选取最优
}
注:wv[i-1][0]表示将放入的物品重量,j表示剩余可放容量,wv[i-1][1]代表价值(之所以wv[i-1][0]中用以这两个条件来填表sheet,最终sheet[number][capacity]即为最大价值。(number物品个数,capacity最大容量)
求出最大容量后,我们在根据上面的两个条件,用回溯法逆推得到所选包的序号。我这里通过Find()函数来找包的序号。
至此,背包问题的最大价值和所选背包都找出来了。
3.具体实现
1.初始化物品的重量和价值:
2.初始化表的基础: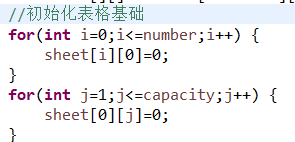
3.填表:
4.得到结果:
5.按照结果回溯:
4.算法时间复杂度分析
(1)初始化物品重量和价值: N
(2)填表:(N+1)(capacity+1)
(3)重新构造wv: 2N
(4)回溯递归: N
(5)输出包序号: N
将其加起来 O(N)=O(k*N) (k是常数)
当然还可以优化,比如,可以去掉重新构造wv等等。还待改进。
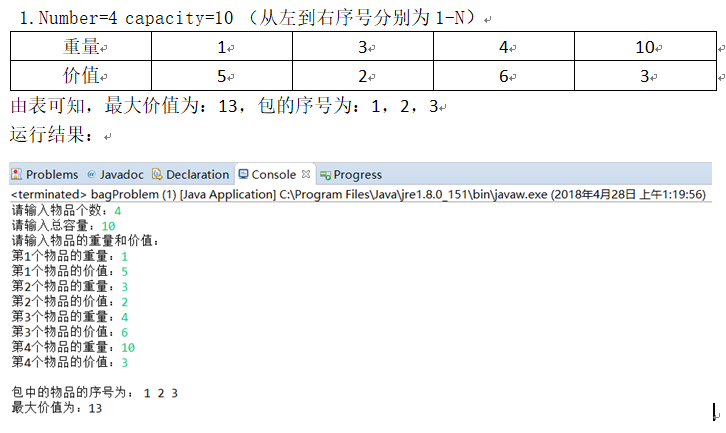
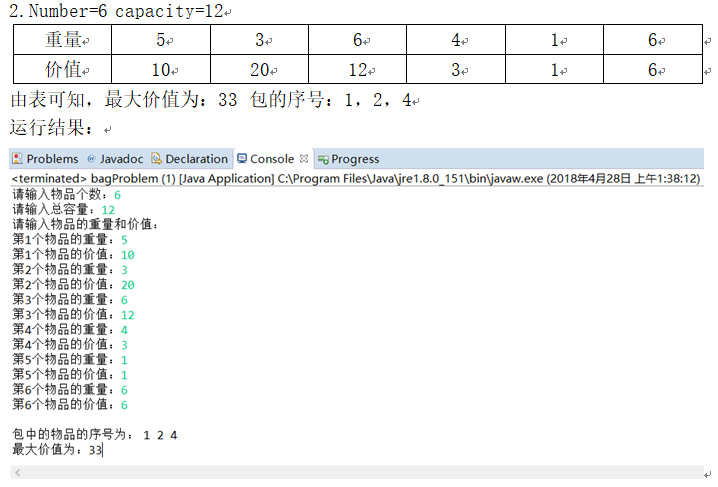
5.运行结果
注:
- 所做的分析都是笔者自己的见解,如有不正确还请见谅。
- 另外,如需代码请访问我的Github:https://github.com/Zxnaruto


