字典序问题

1.问题描述

     在数据加密和数据压缩中常常需要对特殊的字符串进行编码，给定的字母表A由26个小写的英文字母组成，该字母表产生的升序字符串是指字符串中字母从左到右出现的次序与字母在字母表中出现的次序相同，且每个字符最多出现1次(例如，a,b,ab,bc,xyz等字符串都是升序的字符串),对于任意长度不超过6的升序字符串迅速计算出它在字典中的编码。现在对字母表A所产生的所有长度超过6的升序字符串按照字典序排列并编码如下：

2.解决办法

     先新建一个字符串数组，包含a-z，然后对数组里的字符按顺序且长度不超过6进行组合，这里用到for循环来进行组合。分别为一个，两个，三个，四个，五个，六个字符为一组。然后将输入的字符串与组合的字符串进行比较，我这里是在进行分组的时候就进行比较，如果找到就退出程序，不进行下面的循环，提高效率。计数则是用count来保存次数，如果输入的在第1个循环中没有则记下它循环的次数，加上下面找到时的位置就可以得出字典序。
     (1)字母分组：是以每次循环的第一个字母为基准，向后添加字母。
     (2) for循环的循环嵌套进行字符串的分组:
      一个字母为一组时自然一个for，进行N次循环（这里N=26）。

      两个字母时：由于两两组合，需要两个for，外层需要N-1次(最后一个字母不能为首字母)，内层需要随i的变化来决定第二个字母是什么，当a为第一个时，第二个只能是b以后的，所以第二层中的j要从下一个起，即随i的变化而加一，又因为要组合到最后一个字母，所以内层循环的控制条件要到N。

     三个字母组合时，需要三个for,最外层需要N-2次(最后一个首字母为倒数第三个)，中间层也需要通过i来控制后一个字母是什么。它的循环控制条件是小于N-1，这是因为它是第二个字母，极限取到数组的倒数第二个，不能再往下取了(否则就不是按顺序了)。最后一层需要上一层的j来控制条件，以及循环控制条件小于N

通过上面三个我们可以得到以下规律：
        //单个字母
		for(int i=0;i<N;i++)

		//两个字母
		for(int i=0;i<N-1;i++)
		for(int j=i+1;j<N;j++)

		//三个字母
		for(int i=0;i<N-2;i++)
	    for(int j=1+i;j<N-1;j++)
		for(int k=1+j;k<N;k++)

		...........
		//x个字母
		需要x个for,
		最外层循环次数：N-(x-1)
		内层循环次数：N-(x-1-1.......) 直到括号中的等于0

		前面控制条件：
		0
		j=i+1
		k=j+1
		l=k+1
		........
		都是前项+1

4.具体实现

1.声明一个数组用来供字母分组用：

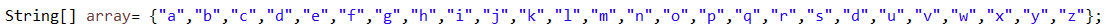
2.对字母进行分组：
   一个字母：(array[i]为 a—z 26个组)

    两个字母：（arrau[i]+array[j]为 ab—yz 325组）

   三个字母：（array[i]+array[j]+array[k]为 abc—xyz 2600组）

………………….

   六个字母：（array[i]+array[j]+array[k]+array[l]+array[m]+array[n]为
abcdef—uvwxyz 230230组）

3.输入字符串str比较，用count计数，得出字符串的字典序

5.算法时间复杂度分析

一个字母O(N)
	   	两个字母：N-1+N-2+N-3.....+N-N
	   	       lim=N^2-2N
	   	       O(N^2)
	   	依次类推：
	   	三个字母O(N^3)
	   	四个字母O(N^4)
	   	五个字母O(N^5)
	   	六个字母O(N^6)

	   	所以，综合，最好T(N)=O(N),最坏T(N)=O(N^6)
	   	这是对N个长度的字符数组且以不超过6个字母排序而言的

        缺点：当基数很大时时间复杂度会很大，所以这是一种效率不高的算法。还有待改进。

6.运行结果

1.运行程序，输入字符串a

2.输入opq

3.输入uvwxyz

注：

• 所做的分析都是笔者自己的见解，如有不正确还请见谅。
• 另外，如需代码请访问我的Github：https://github.com/Zxnaruto

赏

Thank you,么么哒

支付宝

微信